speculative nonfiction
Not so byzantine algorithm studies: Using math to deliver your medication
Like many commercial software developers, math plays a more sporadic role in my day-to-day work. That said, I certainly wouldn’t blithely demote knowing math below other techs like programming languages, web frameworks, and principles of software design/architecture; which already sets up a false dichotomy, anyway.
Math presents a beautiful core proposition to software developers. Through its powers of abstracting and reducing real-world dynamics into expressable, repeatable, sequential logic – which we can be lifted easily into our favorite coding grammars – math can be the companion dynamo we need for achieving levels of faithful verisimilitude for real world complexities (Keep It Savvy Stupid).
Italicizing knowing math is totally an intentional problematization to mess with the idea that knowing math is narrowly scoped to demonstrating technical prowess of calculation or proofing. I think software engineers can, and should, consider a relationship with math as knowing enough math; like, an ontological relationship with math’s formalism and general principles. Math The Good Parts, so to speak. Otherwise the bravado of equating math and problem solving or math as “hard” (dick) science of some kind is doomed to engender an axiomatic blur that will gate keep devs who are not deemed fit for lack of educational background or interest in fiddling with greek letters. Keep these gates wide open, por favor!
(I also think the focus on calculation in my early schooling, alienated from everyday material uses, made me quite Meursault for it – perhaps why I don’t feel the need to champion for being mathy. It took entering commercial software life much later in life to see how the dynamo helps us make stuff and therefore able to consider embracing math (and being embraced by math) again.)
Our praxis: we can coopt knowing math to ramify similar to our desire for Senior Engineers™ to be T-shaped with their knowledge of the stack in order that they can press more heavily on architecture and design. For example, we can desire for React developers to:
- Understand just enough graph theory to see component architectures as graphs;
- Understand the implications of data pipelining and message passing in a graph (bonus points for being a student of Christopher Alexanders' semilattices)
- Or understand just enough category theory to understand the heritage and benefits of composability of first-class functions – is JS even fun without a bit of FP? What else?
This is all just to say that some business problems map really well to higher-order maths and devs should be prepared for it, at least through the design phase. Again, once we sit down to write code, we can easily offload the fastidious implementation details; those few lines of copy|paste from the math deep state.
For example, take a common e-commerce retail problem like Distributed Order Management (DOM). Modern omnichannel selling combined with cloud computing open a broad field of possibilities to achieve low-cost order fulfillment. Affine cost structures – resulting from variable/variadic shipping dynamics – will increase complexity as an ecommerce company scales. We’re talking about quite a bit of real-world complexity to model and adapt to.
What, then, when we’re tasked to create an algorithm to satisfice a version of this problem where you have these rough requirements:
- Orders must be completely fulfilled
- There will be variant shipping costs per supplier
- Orders can be fully splittable by a supplier
This kind of thing will break your brain once you start to grasp for a rational boundary to contain the argument ramifications: supplier availability, supplier inventory availability, etc…
I was presented with a challenge like this recently and it took me a couple hours just to understand what this problem domain was; like, find my way to DOM through off-by-one google searches; a true StumbleUpon revival. Because I didn’t know the math well-enough yet. Google is pretty fast though, and within minutes I practically broke out in a sweat after discovering multiple long-winded computer science papers written on the topic filled with intimidating mathy notations. Then more OMGs and mon dieus as I careened sharply into Cantor’s theorem and Set Theory. Wait, am I doing math? Oh mersault!
More and more it seemed a fantasy that I’d be capable of solving Amazon within a reasonable amount of time because this gestalt was increasing aggressively. Nonetheless, after some deep breaths and patience recoup and having worked with enough devs without math experience, I began to inculcate to this world and realize any solve was going to be an approximation of some sort and probably wouldn’t require me to crack open a text book; there was no silver bullet or excavation of secret proofs. Rather, this whole class of optimization maximations applied to fulfillment problems is a rigorous academic field, but when it meets the metal it softens and warms for Good Enough™️ programming. Each potential brute force linear assignment or dynamic programming algorithm was discarded. My inputs couldn’t be structured into a decision table or cost matrix amenable to path finding, traversal, or Cartesian production. Which meant I could rule out potentials like Kuhn’s Hungarian algorithm. In fact, the scope was something more akin to a set cover or networking problem – still a brave new world, but less and less unbounded the more I scoured the web. Ulimately, my task was gonna be something toward imagining all probabilities between order items and suppliers, and then reducing these matches against cost constraints. “All probabilities” was a strong clue.
So, a bit surprisingly for someone not used to needing math everyday – and certainly not trying to fuck with this:
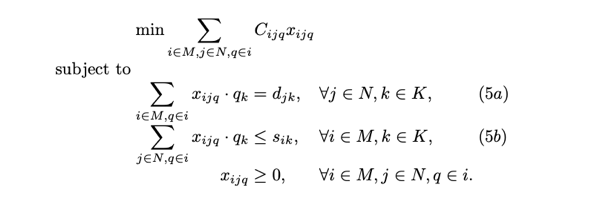
I soon found myself drifting at a comfortable altitude through Probability and Combinatorics with the help of other cow path pavers – we are community-taught developers, after all! – crafting a studied, yet heuristic, approach from where I could thread my inputs through techs like combinations and permutations to make some educated guesses.
The general step-rules of algorithm gradually accreted into something resembling following:
- Generate all possible combinations of order items
- Order items are unique, therefore we are working with a Set. We can therefore use a mathematical definition of a Powerset and create a function which outputs a set of all subsets of any set S:
powerset([A, B, C]) === [[A], [B], [A, B], [C], [A, C], [B, C], [A, B, C]]; - Generate all possible combinations of combinations order items that are less than or equal to the number of suppliers
- Effectively take the result of the Step 1 as the input Set for another powerset that only returns combinations of order item splits that can be fulfilled by available suppliers. For two suppliers:
powersetBySize(powerset([A, B, C]), 2) === [ [["A"]], [["B"]], [["A"], ["B"]], [["A", "B"]], [["A"], ["A", "B"]], [["B"], ["A", "B"]], [["C"]], [["A"], ["C"]], [["B"], ["C"]], [["A", "B"], ["C"]], [["A", "C"]], [["A"], ["A", "C"]], [["B"], ["A", "C"]], [ ["A", "B"], ["A", "C"], ], [["C"], ["A", "C"]], [["B", "C"]], [["A"], ["B", "C"]], [["B"], ["B", "C"]], [ ["A", "B"], ["B", "C"], ], [["C"], ["B", "C"]], [ ["A", "C"], ["B", "C"], ], [["A", "B", "C"]], [["A"], ["A", "B", "C"]], [["B"], ["A", "B", "C"]], [ ["A", "B"], ["A", "B", "C"], ], [["C"], ["A", "B", "C"]], [ ["A", "C"], ["A", "B", "C"], ], [ ["B", "C"], ["A", "B", "C"], ], ]; - Generate all permutations of suppliers
- Generate all viable routes by matching between the sized combinations of order items (result of Step 2) to supplier permutations (result of Step 3)
- Basically a fancy zipping computation
- Filter viable routes against both superficial and business constraints like like duplicated suppliers and supplier availability and/or inventory
- Compute the lowest cost route!
Now there’s a well-suited mathy modeling!
Some other thoughts
Combinatoric applications for this algorithm are quite expensive: you can see how the cardinality flourishes pretty fast above, and my example is for a modest 3 order items and 2 suppliers. If those numbers increase by any measure CPU will be tremendously exercised. (I believe the runtimes of these functions may be polynomial?) I can see why optimization becomes an attractively ripe apple for academicians. Quickly glossing, I can imagine optimizing the looping functions to break before completion when satsificing within a range of acceptance criteria; or structuring the data as Iterators and/or piping through transducers to minimize space complexity with lazy or eager techniques.
By the way, JS has pretty underwhelming options for combinatorics. I found one library that I found a bit awkward to use and ended up ditching in favor of a few standalone implementations of powerset and permutations so I could ensure the code would comply with how I was trying to express the above heuristic. Unsurprisingly, Python’s itertools has combinatoric functions built in and even provides recipes for common tooling you can build on primitives like permutations() and combinations(). For example, powerset().
def powerset(iterable):
"powerset([1,2,3]) --> () (1,) (2,) (3,) (1,2) (1,3) (2,3) (1,2,3)"
s = list(iterable)
return chain.from_iterable(combinations(s, r) for r in range(len(s)+1))
Or simply import the blessed more-itertools library. Of course, this is expected for Python which is heavily developed for the data science world.
Wednesday September 9, 2020